Voici une représentation de la sphère unité obtenue en saisissant 2000 pour le nombre de points à créer et 0.05 pour l'épaisseur.
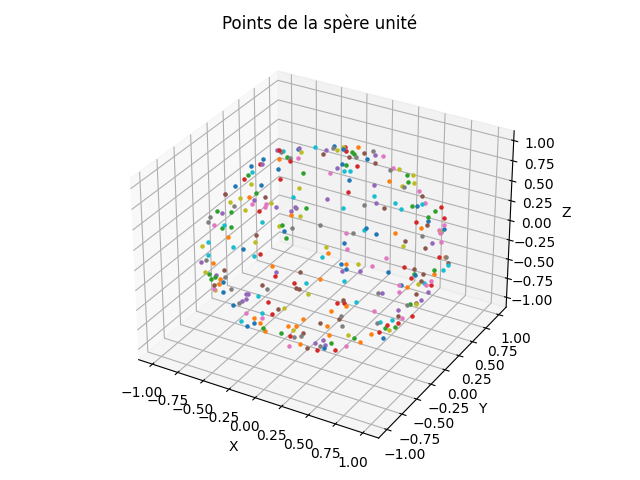
En jouant sur la couleur des points, en fonction d'une de leurs coordonnées, on parvient à mieux rendre compte du relief.
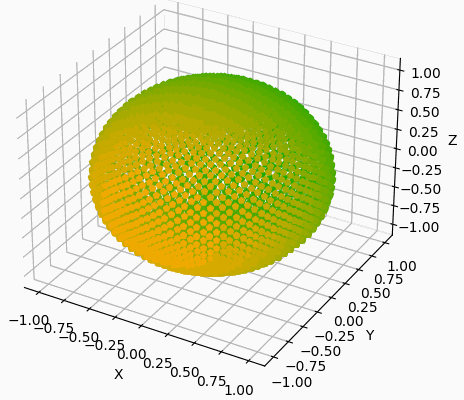
Une représentation de géographe
Pour représenter la Terre et pour localiser un lieu à sa surface, il a été créé un réseau de parallèles et de méridiens.
Quelques définitions :
- Un méridien est un demi grand cercle imaginaire tracé sur le globe terrestre reliant les pôles géographiques.
- Un parallèle est un cercle imaginaire de la sphère terrestre, parallèle au plan de l'équateur, servant à mesurer la latitude.
Idée à exploiter :
On se propose dans cette partie de représenter la sphère par ces lignes si utiles aux géographes.
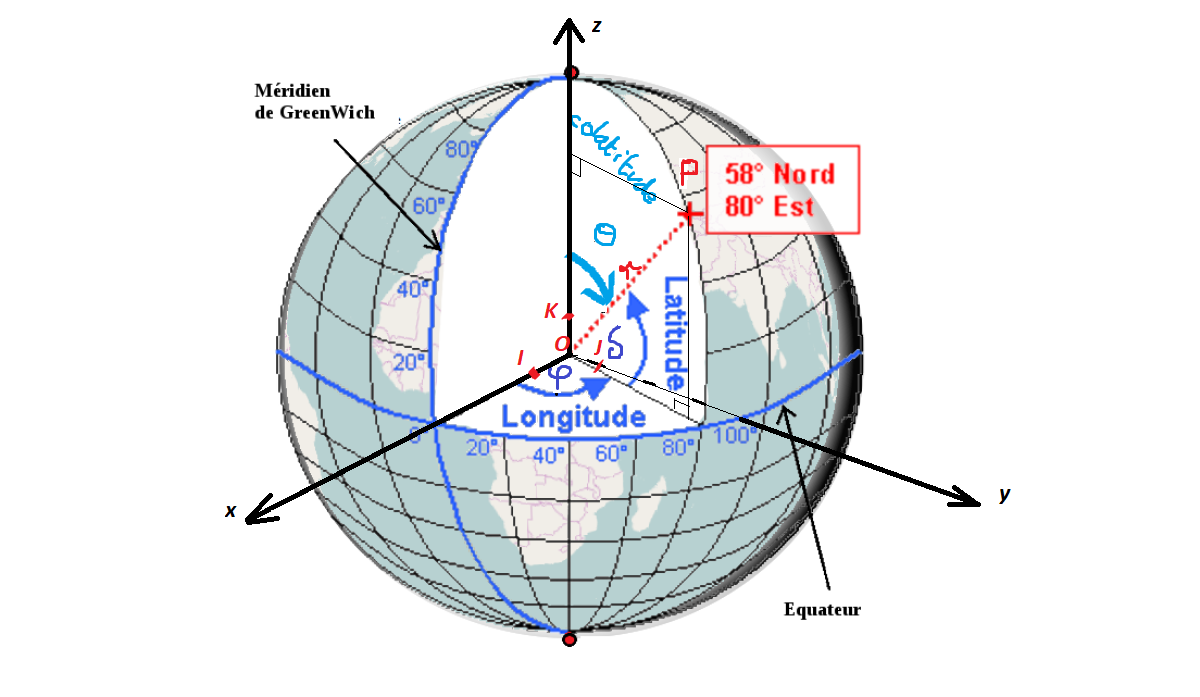
La position du point P sur une sphère est généralement définie par la distance r et par les angles θ (colatitude) et φ (longitude). Mais les géographes utilisent la latitude notée δ , la longitude φ et l'altitude mesurée par rapport au niveau de la mer ou à une ellipsoïde de référence.
Les coordonnées d'un point quelconque de la sphère unité (r=1) ne dépendent donc que de deux paramètres φ et δ.
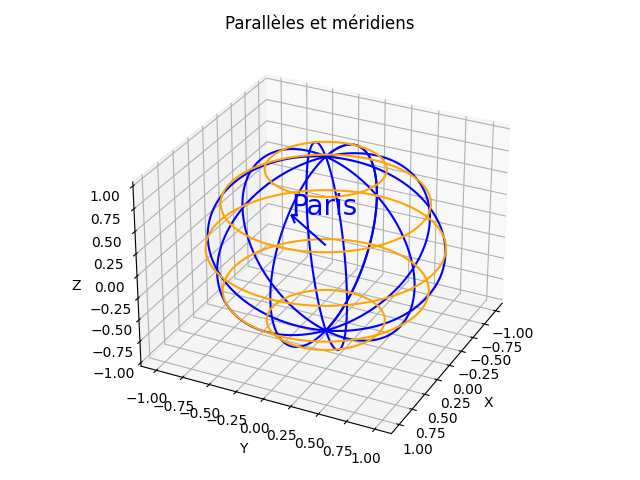
Voici le code Python, ayant permis d'afficher des parallèles et des méridiens, ainsi que la position de Paris à partir de sa latitude et sa longitude exprimées en degré.
# importation des bibliothèques mathématiques et graphiques ou de fonctions des bibliothèques
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import numpy as np
from numpy import pi, cos, sin
#Préparation de la figure en perspective
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
#Méridiens
p = np.linspace(-pi, pi, 15) # p est une liste de 15 nombres régulièrement répartis dans l'intervalle [-pi, pi]
delta =np.linspace(-pi, pi, 100)
for phi in p:
x = cos(phi)*cos(delta)
y = sin(phi)*cos(delta)
z = sin(delta)
ax.plot(x, y, z, )
#Parallèles
phi = np.linspace(-pi, pi, 100)
t =np.linspace(-pi, pi, 15)
for delta in t:
x = cos(phi)*cos(delta)
y = sin(phi)*cos(delta)
z = sin(delta)
ax.plot(x, y, z, )
#latitude de Paris en radians
delta=48*pi/180
#longitude de Paris en radians
phi=2*pi/180
# vecteur d'origine O pointant sur Paris
ax.quiver(0,0,0,cos(phi)*cos(delta), sin(phi)*cos(delta), sin(delta),length=1.0, normalize=True, color='blue', arrow_length_ratio=0.15)
# texte à l'emplacement de Paris
ax.text(cos(phi)*cos(delta), sin(phi)*cos(delta), sin(delta), 'Paris', fontsize=20, color='blue')
# affichage
plt.title("Cordonnées sphériques")
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.tight_layout()
plt.show()
Le système constitué des expressions de x, y et z, en fonction de φ et δ permet une paramétrisation cartésienne de la sphère. Il en existe bien d'autres, que l'on peut visualiser par leurs lignes de coordonnées. De façon générale, la paramétrisation, d'une courbe, d'une surface est une chose très importante en mathématiques et en sciences.
Une représentation en biologie
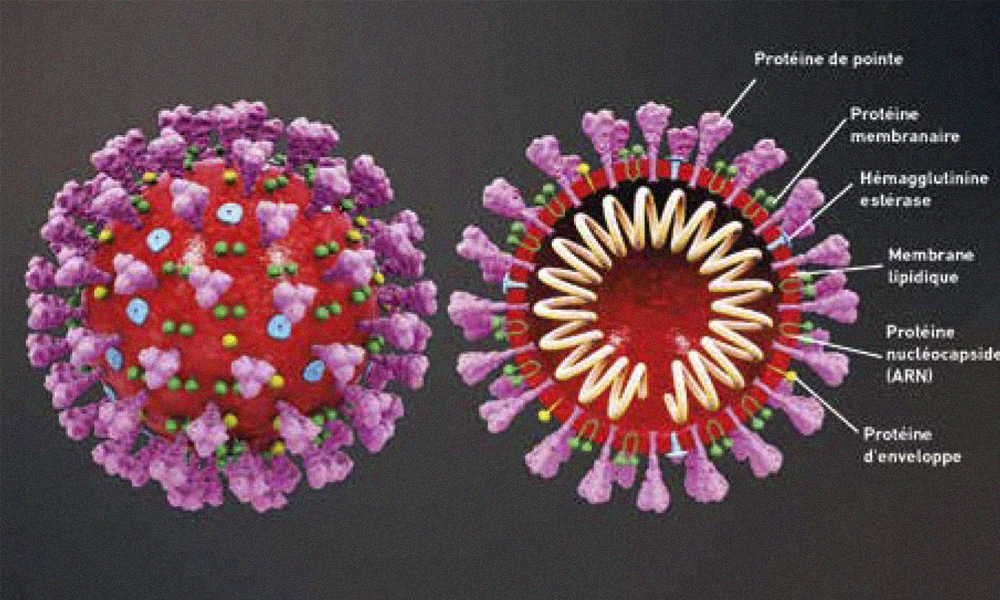
Ci-dessus est représenté le SARS CoV-2 et sa protéine pointe (spike). Celle-ci semble régulièrement répartie à la surface du virus et l'on souhaiterait obtenir une telle répartition sur une figure obtenue en Python. La première méthode aléatoire ne permet pas de dessiner un nombre souhaité de protéine pointe et la deuxième doit être retravaillée, afin que la répartition des protéines à la surface du virus paraisse à la fois régulière et naturelle.
Idée à exploiter :
On va placer un seul point par parallèle, afin de pouvoir les dénombrer et tenter de les répartir harmonieusement en longitude.
Du nombre d'or à l'angle d'or
Le nombre d'or φ, qui évoque l’harmonie des proportions et l’esthétique dans les arts est déjà présent dans les Eléments d'Euclide.
Partageons un disque en deux secteurs angulaires tels que la mesure du plus grand angle a divisée par celle du petit angle b soit égale au nombre d'or φ. Le plus petit angle b sera appelé l'angle d'or.
Nous allons réutiliser les mêmes notations que dans la partie précédente.
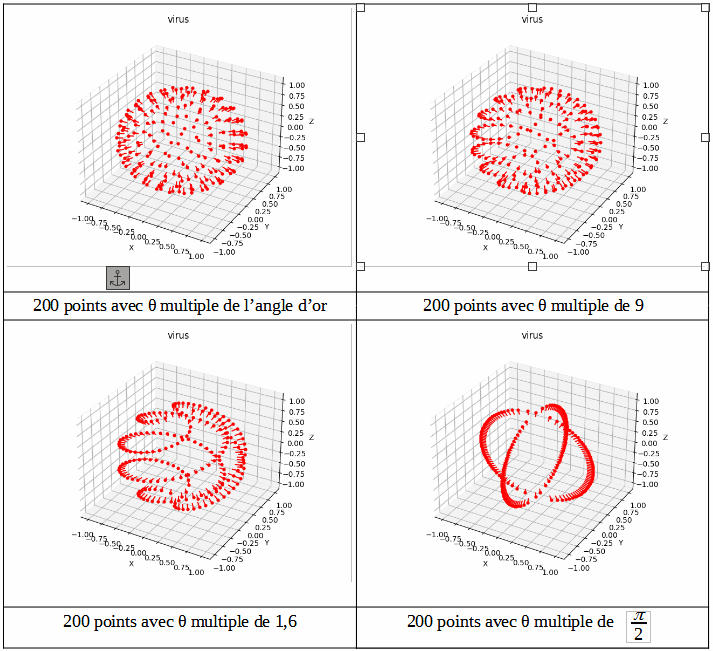
Nous souhaitons maintenant placer nb points répartis de façon harmonieuse et naturelle à la surface d'une sphère unité. Pour cela,nous allons créer une liste de nb nombres compris entre -1 et 1 qui seront les hauteurs des points à placer sur la sphère et à chaque valeur, nous lui associerons un multiple de l'angle d'or qui deviendra l'angle φ permettant le placement du point sur la sphère.
La répartition des 200 points à la surface de la sphère obtenue avec l'angle d'or est harmonieuse et naturelle et pourrait permettre la modélisation du SARS CoV-2. D'autres valeurs permettent également un rendu naturel, mais nous remarquons que la répartition n'est pas la même en fonction des valeurs de φ choisies et certaines sont très régulières ou curvilignes et ne correspondraient pas du tout à la représentation de la surface du virus.
Vous pouvez essayer d'autres valeurs et observer les répartitions obtenues
Le cylindre
Un cylindre d'axe (d) et de rayon r est l'ensemble des points situés à la distance r de l'axe (d). Tout plan perpendiculaire à l'axe coupe le cylindre en un cercle de rayon r et toute droite parallèle à (d) situé à une distance r de (d)est sur le cylindre.
Idée à exploiter :
Représenter ces cercles (parallèles) et ces droites (méridiens).
Nous allons représenter le cylindre d'axe (Oz) et de rayon 1, avec z évoluant dans l'intervalle [-1, 1].
Soit M un point de ce cylindre situé à la hauteur h du plan (Oxy), le projeter sur le plan (Oxy) parallèlement à (OZ) en H.
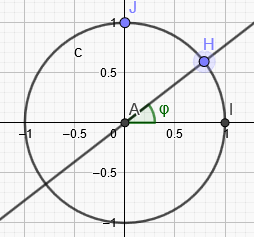
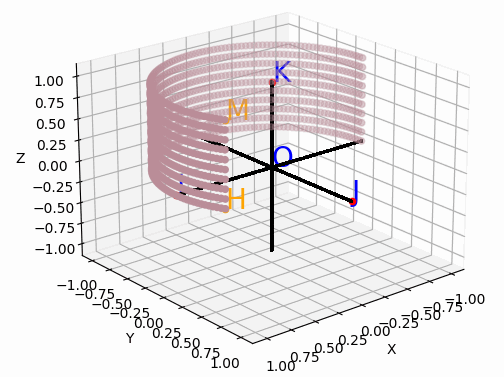On notera φ la mesure de l'angle formé entre l'axe (Ox) et (OH). On a alors cette figure :
Le cône
Dans cette partie, il faudra représenter un cône de révolution d'axe (Oz) et de sommet O. Soit (d) une droite coupant (Oz) en O. Le cône de révolution d'axe (Oz) généré par (d) s'obtient par la rotation de (d) autour de l'axe (Oz), la section de ce cône par un plan perpenciculaire à (d) est donc un cercle. (d) est appelée droite génératrice de ce cône.
Idée à exploiter :
Représenter les cercles (parallèles) dont les centres sont des points de l'axe (Oz) ou des génératrices.
On utilisera cette propriété : ces cercles ont des rayons r proportionnels à la hauteur h de leur centre. On prendra ici r=0,5h
Soit M un point de ce cône de révolution d'axe (Oz) généré par la droite (bleue)(d) et situé à la hauteur h du plan (Oxy), le projeter sur le plan (Oxy) parallèlement à (OZ) en H. On notera φ la mesure de l'angle formé entre l'axe (Ox) et (OH), comme pour le paramétrage du cylindre.
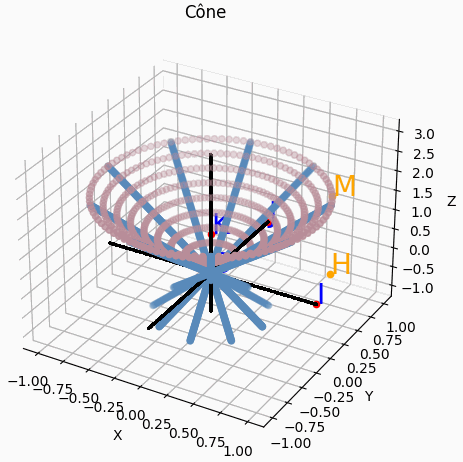
En Bonus : les côniques
Les cercles (parallèles) que l'on a construits sont des intersections de plans orthogonaux à l'axe (Oz) et du cône.
Les génératrices s'obtiennent comme intersections
de plans contenant l'axe (Oz) et du cône.
On va continuer à couper ce cône par des plans passant par le point A(0,0.5,1)représenté en vert, ainsi l'on pourra construire
une ellipse, une hyperbole et une parabole. Ces courbes sont appelées côniques. Remarque : le cercle s'obtient par intersection d'un plan et d'un cône,
c'est donc aussi une cônique. Un cercle est aussi une ellipse particulière.
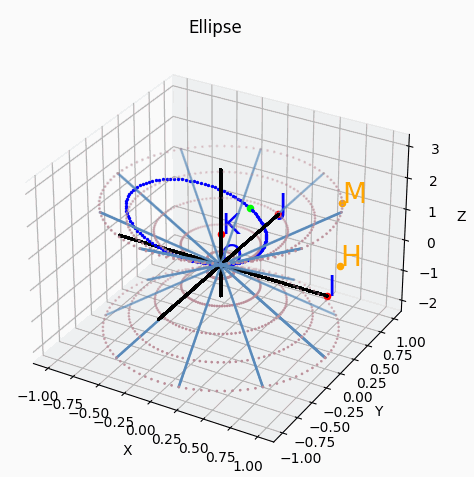
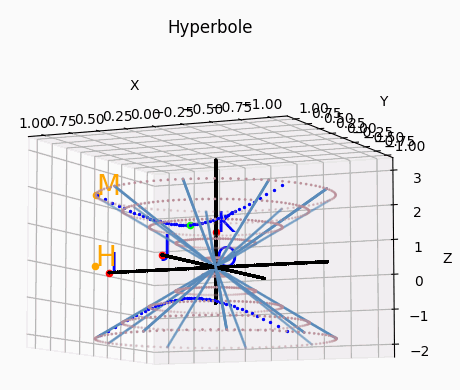
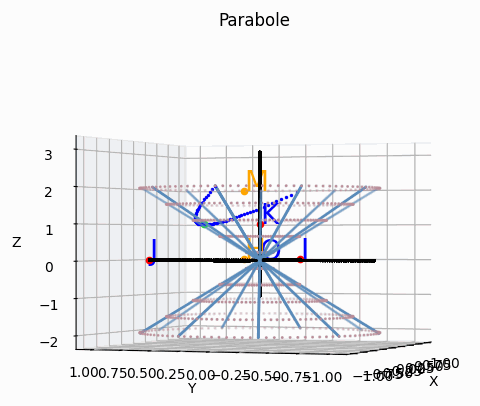
Cas des côniques dégénérées : se produit quand le plan contient le sommet du cône O.
Si l'angle d'inclinaison du plan avec l'axe du cône est nul, c'est à dire si le plan contient (Oz), on obtient une cônique dégénérée constituée de deux génératices.
Si l'angle d'inclinaison du plan avec l'axe du cône est égal à α, l'angle formé entre une génératice et l'axe du cône, on obtient une cônique dégénérée constituée d'une seule génératice.
Si l'angle d'inclinaison du plan avec l'axe du cône est droit (mais pas seulement), on obtient une cônique dégénérée ne contenant que le sommet O.